Perfect Shuffles
Description
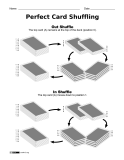
Card magicians have long known that if you can perform a "perfect shuffle" then you can make it appear like you're shuffling the cards into a random order while you are actually controlling where the cards are going. The most well-known example of this is that if you perform 8 perfect shuffles on a standard 52-card deck, the cards will return to their original order.
But there's a more interesting aspect of perfect shuffles that requires knowledge of binary numbers. If you want to take the top card in a deck and shuffle it down to a particular position, all you need to know is the binary representation of the position where you want the card to go. Then you perform a sequence of 'in' and 'out' perfect shuffles based on the binary number and the card will be shuffled into the desired location.
These worksheets first describe the two kinds of perfect shuffles and then ask the student to track the top card through a sequence of shuffles. 'In' shuffles are abbreviated as 'i' and 'out' shuffles as 'o' and a sequence of shuffles like 'in-in-out' is abbreviated as 'iio'.
While binary numbers are not mentioned on any of the worksheets, the students should discover that a shuffling sequence like 'iio' moves the top card into the position 6 (binary 110). If this is presented in class after binary numbers have been taught, the students should be able to recognize the pattern themselves.
Prerequisites
- Basic familiarity with binary numbers
Documents
 |
|
 |
|
 |
Credits
This is a fairly well-known trick from long ago that card magicians (and card cheats!) have used for a long time.
These documents were created by Gary Kacmarcik and are licensed under
a 
Creative Commons Attribution-Share Alike 3.0 Unported License